Aerodynamics is a discipline filled with optimization problems. Whether it is drag, lift or downforce, an aerodynamicists’ goal is to maximise the potential performance of an object within a set of constraints. To achieve this, the typical approach is to change an input variable and analyse the effect on the output. However, a more efficient way to solve optimization problems is to identify the changes required to the input to achieve the desired effect on the output, known as the adjoint method.
The Adjoint Method
The adjoint method is a mathematical technique that efficiently calculates the gradient of a function. In this way, the search direction or sensitivity of this function is also calculated and can then be used together with a gradient-based optimization algorithm to define a new point. The gradient of this new point is then calculated, and the process is repeated until the maximum or minimum of the function is found, which represents the optimum solution.
To run through an example of how the adjoint method can be used to find the optimum camber and angle of attack of an airfoil for the maximum lift/drag ratio, check out our blog on the adjoint method.
The adjoint method is based on the adjoint equations which are linear differential equations that relate the desired change in output to the necessary change in input. In CFD solvers, adjoint algorithms first solve the primal equations which are the Navier Stokes equations. The algorithm then solves the adjoint equations which requires a process of discretisation, linearisation and iteration. There are two different approaches to this: 1) continuous adjoint and 2) discrete adjoint.
Continuous adjoint generates the adjoint equations from the primal equations analytically first and then discretises and solves them. Whereas discrete adjoint discretises the primal equations before linearising and solving to get the discrete adjoint system of equations.
Continuous Adjoint
The continuous adjoint method offers a number of advantages over discrete adjoint, an important one being the lower memory and CPU cost. ‘With continuous adjoint you don’t need to store the Jacobian matrix, whereas in discrete adjoint you do,’ highlights Pavlos Alexias, Senior CFD Developer at Engys.
‘This matrix takes up large amounts of memory because it contains all the derivatives of the fields, w.r.t. the design variables. Also, discrete adjoint typically uses automatic differentiation tools which lead to memory overheads that slow down the code and increase its complexity. In comparison, continuous adjoint consumes less CPU power and memory which means it can solve faster.’ This allows continuous adjoint to scale easier to more complex problems, such as external aerodynamics, without being that constrained by the number of cells in a computational grid.

Another difference is that discrete adjoint requires duality. In other words, if the primal doesn’t converge, some additional effort is necessary to converge the solution. ‘For continuous adjoint, you don’t need to have a fully converged primal and can use techniques such as field averaging to resemble the primal solution,’ explains Alexias.
‘For example, typically you wouldn’t be able to converge a car in low residuals in a steady-state simulation due to vortex shedding and this would make the usage of discrete adjoint very cumbersome. Whereas continuous adjoint can be deployed in such a scenario without issues.’ ‘This is why, with continuous adjoint, you can easily use a high-fidelity unsteady DES [Detached Eddy Simulation] simulation for the primal problem, average the fields and then solve the equivalent steady adjoint version. Of course, as an alternative, both methods can be used to solve a fully transient primal and adjoint simulation, but this has its own known drawbacks for both.’
‘It’s this efficiency and flexibility that has bought significant benefits to customers, particularly on the roadcar side as it enables them to reduce turnaround times which is key when iterating through designs,’ continues Alexias.
‘From a software development perspective, I find it easier to implement new capabilities with continuous adjoint as existing, primal, algorithms can be re-used for the added adjoint equations. Another nice thing is that with continuous adjoint you get the physical understanding of the adjoint system since the equations and their boundary conditions are in closed form.’
It is also very stable and flexible which is why Engys integrated continuous adjoint into its HELYX software and became the first company to offer a CFD adjoint solution to the market.
Utilising Continuous Adjoint
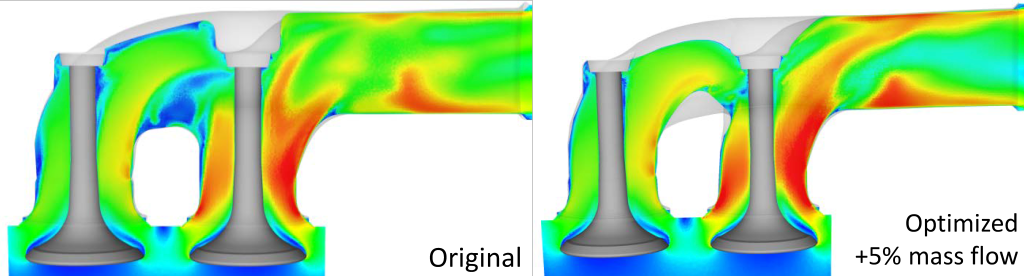
Once the continuous adjoint equations are solved along with the Navier Stokes equations, the surface and volume sensitivities can then be computed. The surface sensitivity calculation results in a coloured surface map which highlights the areas on the surface that need to be moved inwards or outwards to minimise drag or increase mass flow, depending on the case. This is ideal for shape optimization where small deformations in the surface can be investigated to improve fluid dynamic performance.
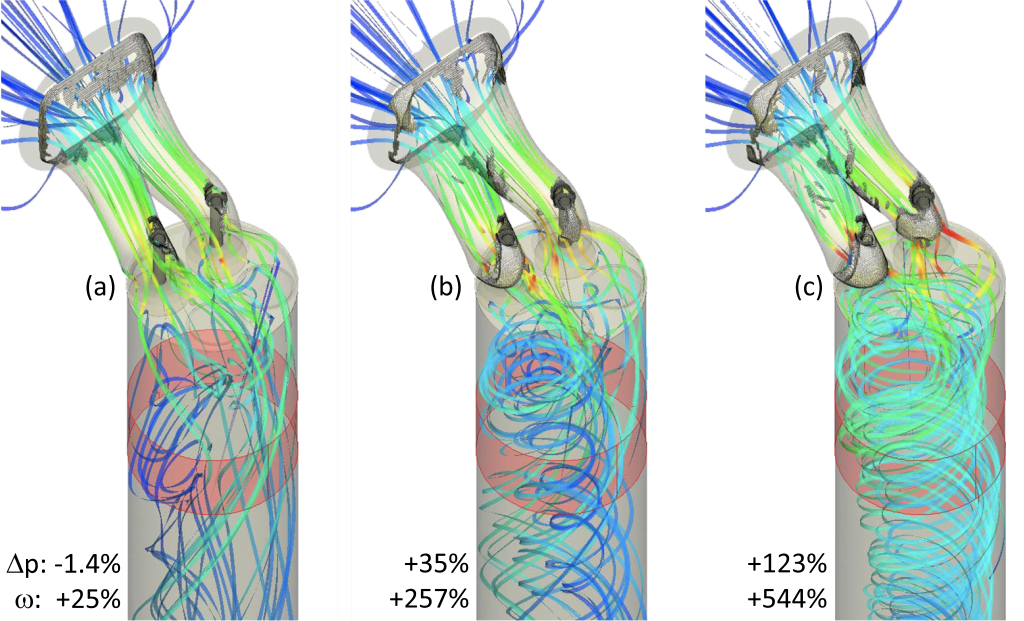
The volume sensitivity calculation also creates a coloured map, but the colours highlight the cells that need to be freed or penalised to minimise pressure drop or increase flow uniformity. This is most suited for topology optimization studies that involve larger deformations.
‘Continuous adjoint offers aerodynamicists the freedom to explore a wider variety of applications,’ says Alexias. ‘Shape optimization can help to reduce drag and improve the lift or downforce of bodywork or propellors in external aerodynamic applications. Whereas topology optimization can be used to minimise the amount of material in a part for lightweighting studies.’
‘In fact, both shape and topology optimization can be used together to improve mass flow, uniformity and swirl control of internal flows in HVAC systems or manifolds. Continuous adjoint is a computationally efficient yet flexible method for solving optimization problems and we’ve only scratched the surface of its capabilities.’